Harnessing the Universal Geometry of Embeddings

Rishi Jha, Collin Zhang, Vitaly Shmatikov, John X. Morris

Cornell University, Department of Computer Science

preprint / code

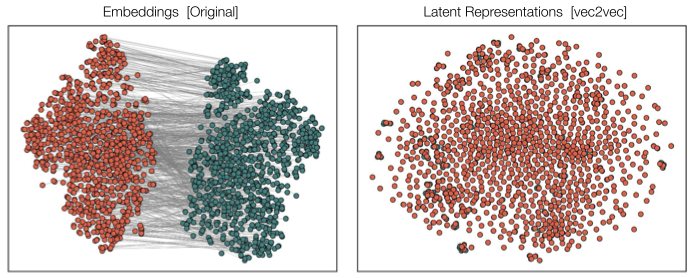Figure 1 Figure 1. Left: input embeddings from different model families (T5-based GTR and BERT-based GTE) are fundamentally incomparable. Right: given unpaired embedding samples from different models on different texts, our model learns a latent representation where they are closely aligned.

Abstract

We introduce the first method for translating text embeddings from one vector space to another without any paired data, encoders, or predefined sets of matches. Our unsupervised approach translates any embedding to and from a universal latent representation (i.e., a universal semantic structure conjectured by the Platonic Representation Hypothesis). Our translations achieve high cosine similarity across model pairs with different architectures, parameter counts, and training datasets.

The ability to translate unknown embeddings into a different space while preserving their geometry has serious implications for the security of vector databases. An adversary with access only to embedding vectors can extract sensitive information about the underlying documents, sufficient for classification and attribute inference.

Strong Platonic Representation Hypothesis

The Platonic Representation Hypothesis conjectures that all image models of sufficient size have the same latent representation. We propose a stronger, constructive version of this hypothesis for text models,

Strong Platonic Representation Hypothesis: the universal latent structure of text representations not only exists, but can be learned and, furthermore, harnessed to translate representations from one space to another without any paired data or encoders.

Our method, vec2vec, reveals that all encoders—regardless of architecture or training data—learn nearly the same representations (Figs. 1 and 2)!

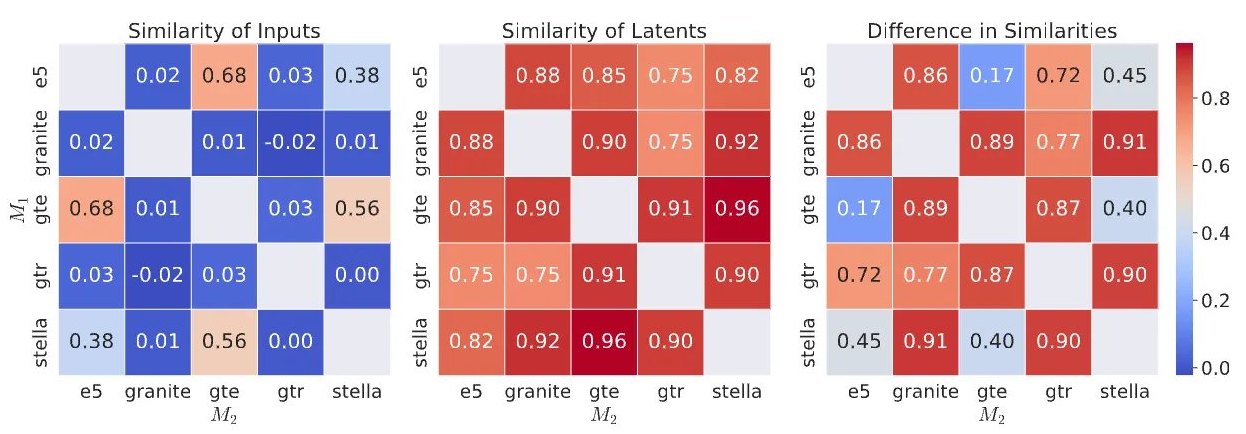Figure 2 Figure 2. Pairwise cosine similarities of input embeddings (left) and their vec2vec latents (middle) across different embedding pairs. The absolute difference between the heatmaps plots is on the right. All numbers are computed on the same batch of 1024 NQ texts.

Preserving Geometry

Leveraging these universal representations, we show that vec2vec can translate embeddings generated from unseen documents by unseen encoders while preserving their geometry: i.e., the cosine similarity of the translated embeddings and the ideal target embeddings is high (Figs. 3 and 4).

The translators are robust to (sometimes very) out- of-distribution inputs indicating that the shared latent structure is not just a property of the training data, but rather a fundamental property of the text embeddings.

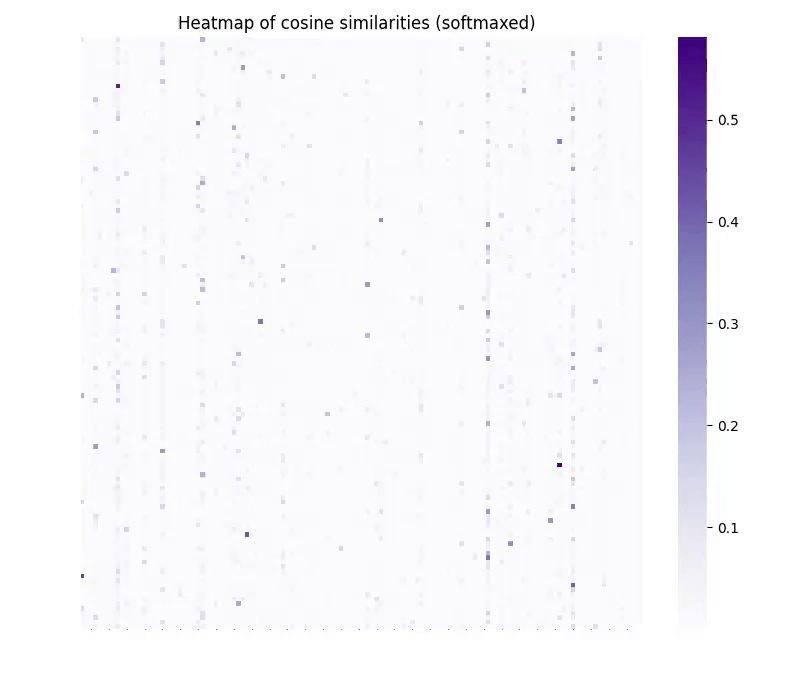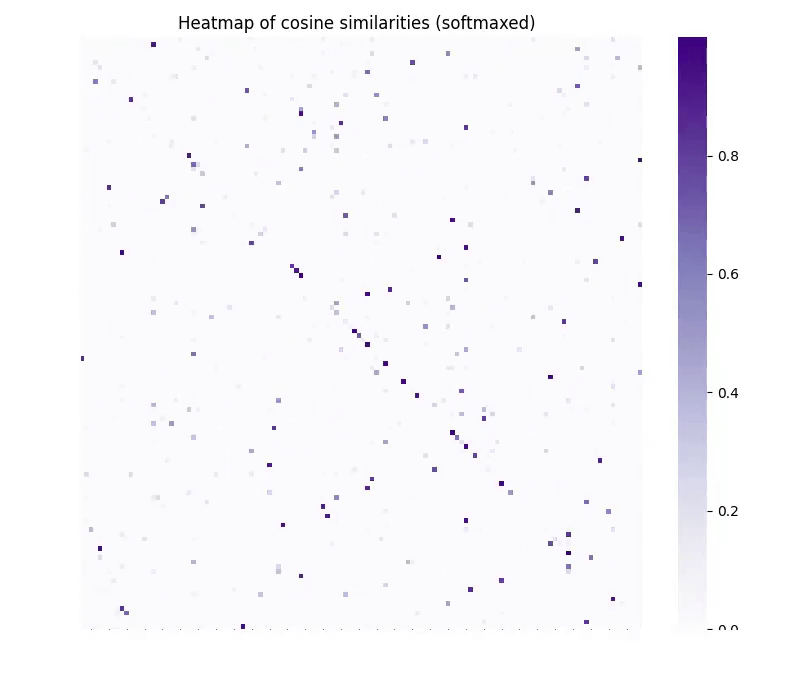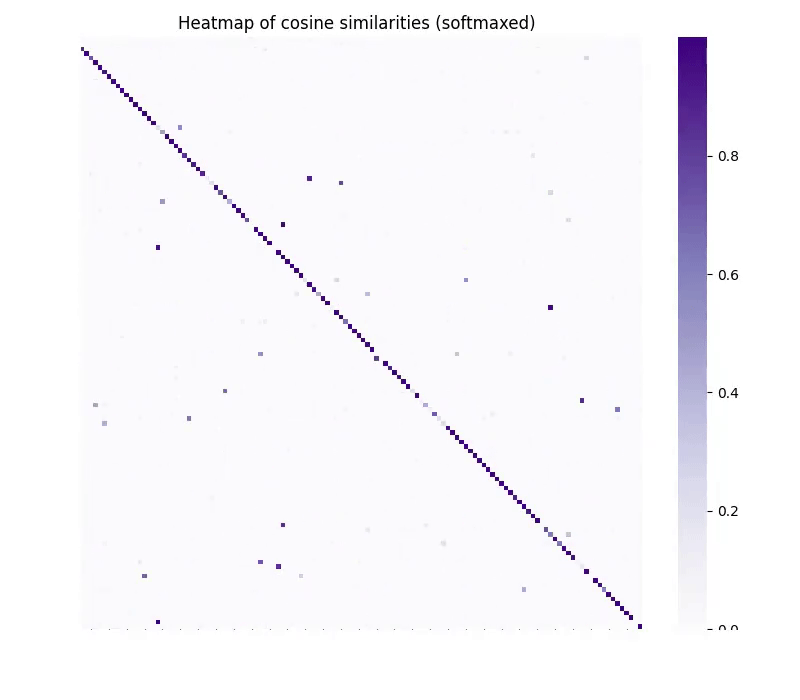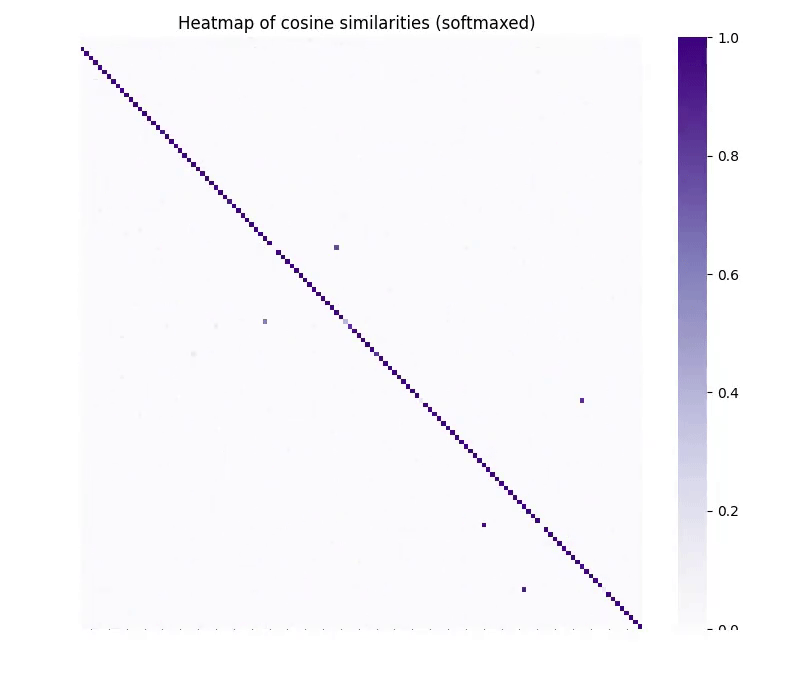Figure 3 Figure 3. Cosine similarity of translated embeddings (y-axis) and ideal target embeddings (x-axis) as a function of the number of training steps. Note that vec2vec does not have access to the target embeddings during training.
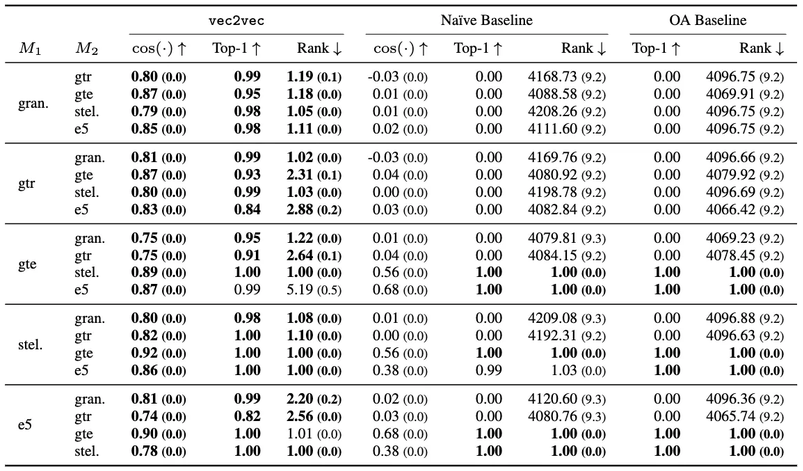Figure 4 Figure 4. In-distribution translations: vec2vecs trained on NQ and evaluated on a 65536 text subset of NQ (chunked in batches of size 8192). The rank metric varies from 1 to 8192, thus 4096 corresponds to a random ordering. Since Optimal Assignment is a matching method, cosine distances are not applicable. Standard errors are shown in parentheses. Bold denotes best value.

Security Implications

Then, using vec2vec, we show that vector databases reveal (almost) as much as their inputs. Given just vectors (e.g., from a compromised vector database), we show that an adversary can extract sensitive information about the underlying text.

In particular, we extract sensitive disease information from patient records and partial content from corporate emails (Fig. 6), with access only to document embeddings and no access to the encoder that produced them. Better translation methods will enable higher-fidelity extraction.

Figure 5 Figure 5. Examples of embedding inversions that infer entities (green) and content (yellow).

Contact & Acknowledgments

If you have questions about this work, contact Rishi Jha at: rjha at cs dot cornell dot edu. The page design was adapted from these two excellent projects: tufte-css and tufte-project-pages.